주성분 분석 (PCA, Principle Component Analysis)

주성분 분석 (PCA, Principle Component Analysis)

주성분이란 데이터에 새로운 축을 긋고, 그 축에 데이터들을 사영 시켰을 때 분산이 큰 축들을 의미합니다. 가장 큰 분산 축을 정하게 되면, 그 다음에는 직교인 축들 중에서 정하게 됩니다.

주성분 분석 (PCA, Principle Component Analysis)이미지 출처: https://en.wikipedia.org/wiki/Principal_component_analysis

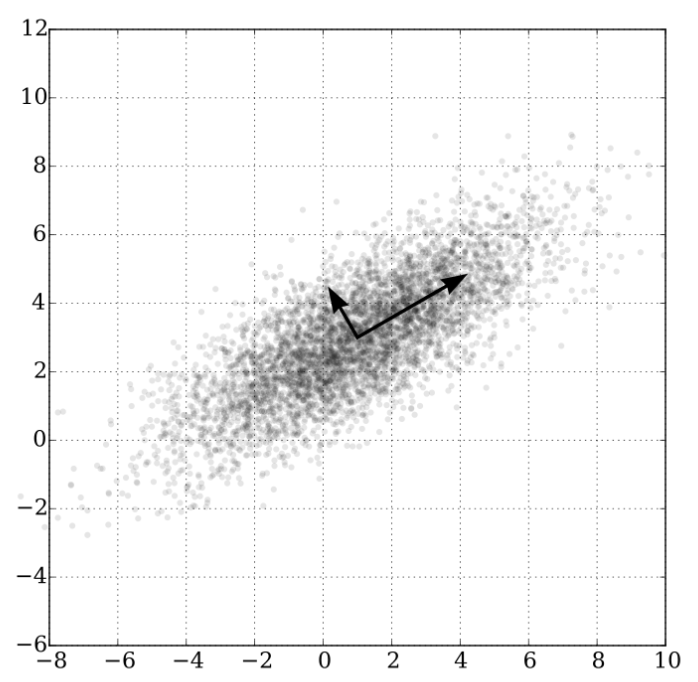
위 이미지는 데이터들의 두 주성분을 나타낸 그림입니다. 오른쪽 위를 향하는 화살표 축을 PC1, 왼쪽 위를 향하는 화살표 축을 PC2라고 해보죠. 그림을 보면 PC1 축에 데이터들을 사영 시킬 때 분산이 가장 클 것으로 예상이 됩니다. 그 다음 PC1에 수직인 축 중 분산이 가장 큰 PC2를 선정하게 됩니다.

주성분 분석 계산을 이해하기 위해 필요한 개념들을 먼저 설명해보겠습니다.
1. 켤레 전치 (Conjugate transpose)
복소수 행렬의 켤레 전치 또는 에르미트 전치(Herimitian transpose)는 그 행렬의 전치 행렬를 취하고 각 성분 별 켤레 복소수를 취하여 얻는 행렬입니다.
$$
A=\begin{bmatrix} 1+2i & 2+3i \\ 4-3i & 1-4i \\ \end{bmatrix}
$$
행렬 A가 있을 때, A의 켤레 전치는 아래와 같습니다.
$$
A^{\ast}=\begin{bmatrix} 1-2i & 4+3i \\ 2-3i & 1+4i \\ \end{bmatrix}
$$
2. 유니터리 행렬 (Unitary matrix)
유니터리 행렬은 복소수 행렬의 켤레 전치가 복소수 행렬의 역행렬과 같은 행렬을 의미합니다.
3. 특이값 분해 (Singular Vector Decomposition, SVD)
m X n 행렬 M에 대하여 다음과 같은 세 행렬의 곱으로 분해하는 것을 특이값 분해라고 합니다.
$$
M=U\Sigma V^{\ast}
$$

특이값 분해

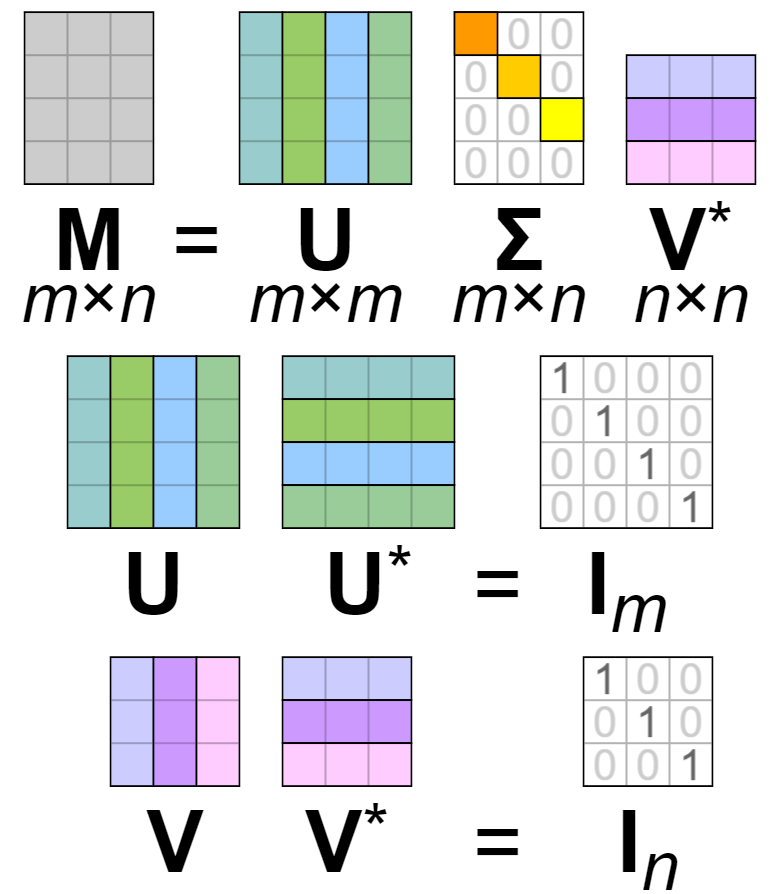
U는 m x m의 유니터리 행렬, V는 n x n의 유니터리 행렬입니다. ∑는 대각 원소만 음이 아니며 나머지는 모두 0인 대각행렬입니다.
m x n 행렬에 M에 대하여 다음 두 조건을 만족하는 벡터 u, v가 존재할 때, 음수가 아닌 실수 sigma를 특잇값이라고 하며 u를 좌측 특이 벡터, v를 우측 특이 벡터라고 합니다.
$$
Mu=\sigma v, u \in K^n, v \in K^m
$$
특이값 분해를 하게 되면, ∑의 각 원소는 특잇값이 되며 이에 대응되는 U의 행벡터와 V의 열벡터는 각각 좌측 특이벡터와 우측 특이벡터입니다.
4. 에르미트 행렬 (Hermitian matrix)
에르미트 행렬이란 자기 자신과 켤레 전치가 같은 복소수 행렬입니다. 실수 원소를 가지는 행렬은 그 행렬의 전치 행렬과 같다면 그 행렬은 에르미트 행렬입니다.
5. 선형 변환
선형 변환은 아래 블로그에 굉장히 잘 설명 되어 있으니 참고 바랍니다.
ratsgo.github.io/linear%20algebra/2017/03/24/Ldependence/
6. 고유값과 고유 벡터
어떤 벡터를 선형 변환 시켰을 때, 같은 벡터의 스칼라배와 같다면 이 벡터를 고유 벡터라 하고 스칼라 값을 고유값이라고 합니다.

그림을 전단 매핑(shear mapping)으로 선형 변환한 예입니다. 파란색 벡터를 위처럼 전단 매핑해도 같음을 알 수 있습니다. 따라서 파란색 벡터는 고유 벡터가 되고, 크기가 같으므로 고유값은 1 입니다. 이미지 출처: https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors

7. 양의 정부호 행렬
에르미트 행렬 M의 모든 고유값이 양수인 경우, M은 양의 정부호 행렬(Positive Definite matrix)라고 합니다.
8. 고유값 분해 (Eigen Decomposition)
특이값 분해에서 행렬 M이 양의 정부호 행렬일 때, M의 특잇값과 특이 벡터는 고유값과 고유 벡터와 같아집니다.
$$
M=V \Lambda V^*
$$
따라서 고유값 분해를 구현할 때 대상 행렬이 양의 정부호 행렬이면 특이값 분해를 하는 np.linalng.svc 함수를 활용할 수 있습니다.

이제 주성분 계산을 해보죠.
1. 데이터를 Zero-centered로 만듭니다.

X -= np.mean(X, axis = 0)

2. Cov matrix를 구합니다.

cov = np.dot(X.T, X) / X.shape[0]

3. Cov의 고유값 분해를 합니다.

U,S,V = np.linalg.svd(cov)

컬럼 U는 Eigen vector가 되고, S는 1-d array의 U의 각 컬럼에 대응되는 Eigen value가 됩니다.

4. 주성분으로 데이터를 사영 시켜 차원 축소합니다.
컬럼 U는 Eigen vector이고 Unit vector입니다. 따라서 X를 Eigen value가 가장 큰 주성분 하나에 사영 시키는 것은 X와 PC1 간 내적과 같습니다 (ratsgo.github.io/linear%20algebra/2017/10/20/projection/ 참고)

Xrot_reduced = np.dot(X, U[:,:1])

X가 1000차원 데이터이고, 이를 100차원으로 줄이고자 한다면:

Xrot_reduced = np.dot(X, U[:,:100])